I believe in Science but I do not believe scientists.
I decided to write this short blog when I read Edg E, Johann et al. (2006) paper on buffering and repeated sprint performance: “Comparison of muscle buffer capacity and repeated-sprint ability of untrained, endurance-trained and team-sport athletes.” It is always interesting how manipulation with statistics can change the conclusions of a study.
When I almost finished my writing, I came across the blog, which was devoted to the correlation mistake in COVID-19 study. Strikingly, the mistake was quite obvious, the study came from quite a famous university (Yale), and it changed the conclusion dramatically: from an almost perfect correlation to R2= 0.15-0.40.
Therefore, I realised that such mistakes, often made in pursuit of the desired result, are quite common in science. Unfortunately, it is often difficult for the general public to see such nuances, therefore false conclusions, and even sensations, may arise.
That is why we should not trust scientists automatically just because they are scientists.
Verification, peer review and criticism are fundamental to the scientific process.
Math and back-squat.
There is a strong positive correlation between back-squat and mathematical abilities in a group of male teenagers!
Most of the sports practitioners who read this announcement probably think, “ This is rubbish!”. Maybe, however, I can do an experiment to prove that.
So teens age is 13-19 years old, right?
I will take two boys for each year (a total of 14), and combine them into one group. Then I will give them a math test and a loaded back-squat. The math test should become progressively easier for older boys. Thus, the older the boys are, the better their math results, because they will have more knowledge. At the same time, seniors will also do better in back-squat because they are bigger and stronger.
I am sure that I will find a pretty strong correlation.
However, common sense tells us, quite rightly, that the relationship between these two qualities is unlikely. So why have I found correlation?
It is because most of us don’t realise that correlation does not necessarily mean a causal relationship.
Math and squat performance are both depend on age, and through that, they are connected with each other. But, unfortunately, being smart in numbering does not help you in weight-lifting.
Repeated sprints and buffering.
In this example, I will show you how looking at correlation from a different angle can completely change the conclusions of the study.
There were three female groups: non-athletes, endurance athletes, and team-sport athletes.
The authors investigated their performance in repeated sprints (RS) and their buffering abilities.
Researchers combined all participants together (as I did with teenagers) and found a positive correlation between the ability to buffer acidosis and performance in 5x 6 sec sprints on cycle-ergometer.
The conclusion is looming that RS depends on the capacity to buffer acidosis.
According to Google Scholar, this paper was cited 118 times, and I am sure that some of the citations stated: “Repeated sprints ability depends on buffering.”
Though authors acknowledged that we should be careful with such a conclusion and there may be other factors involved.
Still, I cannot avoid feeling that they a bit push me to admit the casual relationship between buffering and RS.
Let’s have a look at the graph.
 Credit: Edg E, Johann et al. (2006)
Credit: Edg E, Johann et al. (2006)
The figure which contains inside it all 19 participants indeed stretches towards up-right. That means a positive correlation (r=0.67 in the study). It is how the authors look at correlation.
Non-athletes are generally more on the lower-left part in the graph. This means that they were worse in sprints and buffering, perhaps because they were simply less trained.
Endurance athletes are generally lower than players, which means that they performed weaker in repeated sprints ( overall work).
Players are more on the right as well, due to having a better buffering capacity.
So does this mean that athletes with better buffering are better in sprints?
Not necessary. For example, players may be better in RS because they were bigger, which is important in the cycle-ergometer test. The authors acknowledged that.
Moreover, in my opinion, this study showed exactly the opposite: being better in buffering does not make you better in sprinting.
Let’s have a look at the graph differently.
 Credit: Edg E, Johann et al. (2006)
Credit: Edg E, Johann et al. (2006)
For that, I pooled participants not in one group but in three homogeneous groups accordingly to sports specialisation.
Now we even don’t need calculations. We can see that two figures which outlined players (red line) and non-athletes (green line) stretch pretty horizontally in parallel to axis X. That means that participants inside these groups, despite having different buffering capacity showed similar performance. The endurance group (blue line) stretches vertically in parallel to Y. Thus endurance athletes, despite showing different performance, had similar buffering.
In fact, none of the three groups showed a relationship between buffering and RS performance.
So what is the problem?
Well, it is basically the same as in my math-squat example: you should be careful while combining heterogeneous participants.
If you want to find a true relationship between two variables, you should control other influences as much as possible.
In the math-squat example, I should take boys of the same age, whereas in Edg E, Johann et al. (2006) study, it would be better to compare athletes of the same sport.
There is another important thing.
When there is a small sample size in the study, which is mostly the case in our field, it is necessary to present individual data for every athlete.
Firstly, because a couple of outliners can dramatically change group statistics. Additionally, coaches are interested in the results of every athlete rather than in abstract group numbers. However, researchers often prefer to confuse practitioners with complicated math, even if there are less than ten people in the study. This may be deceptive.
In the present study, there were 6; 7; and 8 people in each group.
The authors did not present individual results in the table, and they did not compare participants within groups. Though, in my opinion, it would be a sensible thing to do. Fortunately, we can derive individual data from the graph.
So thoughtful and attentive practitioners can follow a common sense, and make their own conclusions.
This conclusion maybe quite the opposite to what was stated in the paper: “the findings of the present study are unique, in that while previous investigations have identified a relationship between buffering… and short (60 s) or long (40min) high-intensity exercise efforts, a relationship between buffering and short (6-s), repeated-sprints (total work, r = 0.67) has also been identified.”
My conclusion is that:
Based on the results of the present study, there are no relationships between 6s x 5 repeated sprint performance on cycle-ergometer and buffering capacity in groups of female team-sport athletes, endurance athletes, and non-athletes.
COVID-19 and poo.
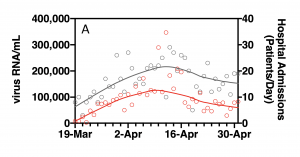
A Yale University study found an almost perfect correlation (R2 = 0.99!) between the amount of viral RNA in sewage and admission to hospital with COVID-19 three days later. You can imagine that this, if true, provides a unique opportunity to pre-prepare beds for the influx of patients.
I have found good explanation of this “sensational discovery” in Alexander Danvers blog.
Authors made the following mistake: they firstly plot both variables against time, smoothened data, and only then compared them between each other. Smoothened plots showed an almost perfect correlation. Instead, they should plot raw data against each other from the start. That gives a much more real correlation: R2= around 0.15-0.4. This range was obtained by automatically extracting data from the graph in the article.
Hospital admission and amount of virus RNA in sewage.
You cannot compare smoothened data (lines) for correlation. You should compare raw data (dots).
Credit: Yale University
Well, I can understand everything. Err… Almost everything.
In the RS study, the researchers used correlation in their own way and entitled to it. Maybe they should analyse the data differently, but this is just my opinion.
Yale scientists can make a simple mistake in statistics, although we may expect a higher standard from this university. What is really surprising is that after getting R2 = 0.99, they did not scratch their heads and said: “Something isn’t right, we should check our results again.” No, instead, they went public.
That is wrong.
Math is a great tool if you use it correctly. However, improper use leads to incorrect conclusions and misleads people who rely on scientists. Sometimes this is the result of errors, but sometimes it is intentional manipulation. Many times I met this phenomenon in the Sports Science. Now I see that perhaps this is a common problem for Science as a whole.
It is a worrying sign.
References.
Edg E J, Bishop D, Hill-Haas S, Dawson B, Goodman C. Comparison of muscle buffer capacity and repeated-sprint ability of untrained, endurance-trained and team-sport athletes. Eur J Appl Physiol. 2006;96(3):225‐234. doi:10.1007/s00421-005-0056-x
SARS-CoV-2 RNA concentrations in primary municipal sewage sludge as a leading indicator of COVID-19 outbreak dynamics. BMJ Yale.